|
Известно, что температурная картина свободной нагретой затопленной турбулентной струи, истекающей в пространство с одинаковой температурой среды, связана с кинематической структурой простым соотношением [1] Δt/Δtx = (v/vx)σ, (1) где σ = 0,65 – 0,7 - турбулентное число Прандтля, Δt – разность температур в струе и окружающей среды, Δtх – то же для температуры на оси струи. Это дает возможность рассчитать температуру струи в любой точке: Δt/Δtx = exp[ - 0,7σ(y/xtgα0,5v)2] (2) Если же струя истекает в пространство с неодинаковой температурой, то ее кинематическая структура не дает простых способов отыскания температурной картины. |
Ю. Н. Марр |
1. Рассмотрим плоскую турбулентную струю, истекающую из сопла шириной bо и размахом Lразм со скоростью vо и температурой tо в пространство, имеющее температуру ta< tо. На расстоянии от сопла примерно 6bо формируется основной участок струи, состоящий из ядра постоянного массового расхода Gя = ρvoboLразм и симметрично примыкающих к ядру зон течения эжектированных масс. Толщина ядра растет вниз по течению в соответствии со степенной аппроксимацией автора зависимости из [2]
δя/bо = 0,328(x/bо)0,362, (3)
где δя – половина толщины ядра, x/bo – гидравлическое расстояние от среза сопла, х/bо = 6…60.
Ядро постоянного массового расхода можно рассматривать как поток в канале с проницаемыми стенками, обменивающийся теплотой с окружающей средой, омывающей канал организованными движениями эжектированных масс. При этом тепловой поток, отводимый через границу ядра, имеет плотность
q = α(tя – ta), (4)
где tя – средняя по сечению температура ядра,
α – конвективный коэффициент теплоотдачи от границы ядра, сформированный всей совокупностью турбулентных движений в окрестности ядра.
Приближение (4) позволяет записать балансовое соотношение
Wяdtя = -2α(tя – ta)dFя (5)
в котором Wя = СрGя – водяной эквивалент ядра, Fя – площадь поверхности ядра плоской струи с одной стороны.
Уравнение (5) преобразуется к виду
dθ/θ = -2dε, (6)
где θ = (tя – ta)/(to – ta), ε = αFя/Wя
Полагая коэффициент теплоотдачи α постоянным на длине интегрирования, найдем интеграл (6) по х/bо от 0 до L/bo
lnΘ = - 2Е (7)
поскольку θ(0) = 1. Здесь Θ и Е – соответственно, значения функций θ(L/bo) и ε(L/bo) в конце участка L/bo. Выражение (7) связывает среднюю на длине L теплоотдачу α к ядру с температурой ядра в конце участка. Используя (2) и (3), а также принимая
tgα0,5v = 0,1, σ = 0,65, получим расчетное выражение для температуры ядра:
Δtя/Δtо = (2,3/√x/bo)exp[ - 45(Yя(δя/bo)/(x/bo))2] , (8)
Yя = y/δя = 0…1, Δtя = tя - tа, Δtо = to-ta
Расчет средней температуры ядра с помощью (8) и подстановка ее в (7) в виде
β = 1/Θ(L) позволяет определить Е и далее α. Выражение (7) в критериальном виде будет
St = lgβ/2(L/bo). (9)
где St = Nu/(RePr) = α/(ρCpvo) – критерий Стэнтона, Nu = αbo/λ, Re = vobo/ν, Pr = ν/a.
Апроксимация (9) дает выражение
St = 0,065 (L/bo) -0,444 . (10)
Таким образом, в привычных обозначениях, средняя по длине струи теплоотдача (число Нуссельта Nu) прямо пропорциональна интенсивности струи (числу Рейнольдса Re) и убывает с увеличением длины струи.
2.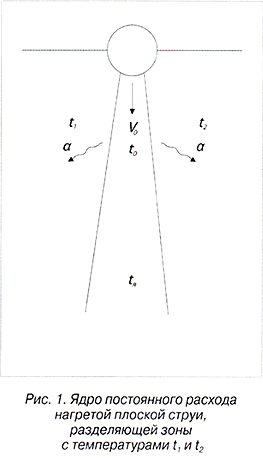 Покажем, как можно использовать (10) в расчетах несимметричной температурной структуры (рис.1). Полагая, что температурная неоднородность не влияет на гидродинамическую картину в окрестности ядра постоянного массового расхода, запишем балансовое соотношение
Покажем, как можно использовать (10) в расчетах несимметричной температурной структуры (рис.1). Полагая, что температурная неоднородность не влияет на гидродинамическую картину в окрестности ядра постоянного массового расхода, запишем балансовое соотношение
Wяdtя = - (tя – t1)αdFя - (tя – t2)αdFя, (11)
или
dθ = (θ2 – 2θ)dε, (12)
где θ= (tя – t1)/(tо – t1), θ2 = (t2 – t1)/(tо – t1), ε = αFя/Wя
Интеграл (12) имеет вид
Θ = 0,5 [θ2 + (2 – θ2)exp(-2E)], (13)
где Е = αLLразм/Wя .
Температура ядра в сечении х = L равна
tя(L) = (tо – t1)Θ + t1 (14)
Пример 1.
Заданы размеры, расходы и температуры:
bo = 0,1м , Lразм = 2м, vo = 15м/с, to = 50oC, t1 = - 30oC, t2 = 20oC, ρo = 1,093кг/м3, Gя = 3,28кг/с, Wя = 3296Вт/К, Fя = 2x м2, θ2 = 0,625
| х, м | x/bo | St | α, Вт/м2К | ε | Θ(L) | tя, 0С |
| 1 | 10 | 0,0234 | 385 | 0,234 | 0,743 | 29,4 |
| 2 | 20 | 0,0172 | 283 | 0,343 | 0,659 | 22,7 |
| 3 | 30 | 0,0144 | 237 | 0,431 | 0,603 | 18,2 |
| 4 | 40 | 0,0126 | 208 | 0,505 | 0,563 | 15,0 |
3. 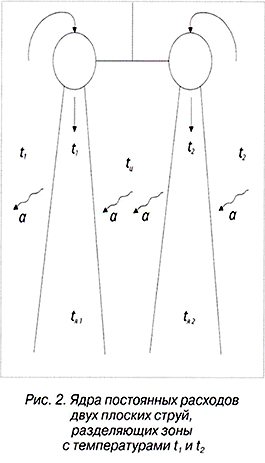 Усложним структуру удвоением струй (рис.2). Предполагается, что межструйное пространство изолировано от областей с температурами t1 и t2. Подача воздуха в струи организована из областей 1 и 2, соответственно начальные температуры струй t1 и t2. Обе струи достаточно удалены друг от друга, чтобы они не сливались на заданной длине и их можно было рассматривать как квазисвободные. Между струй формируется пространство циркуляции масс воздуха, эжектируемых внутренними сторонами струй. Сложный характер направленных движений в циркуляционном пространстве в сочетании с турбулентностью допускает считать там температуру воздуха tц близкой к постоянной. Записывая относительно каждой струи балансовые уравнения вида (11) и преобразовывая их, получим систему
Усложним структуру удвоением струй (рис.2). Предполагается, что межструйное пространство изолировано от областей с температурами t1 и t2. Подача воздуха в струи организована из областей 1 и 2, соответственно начальные температуры струй t1 и t2. Обе струи достаточно удалены друг от друга, чтобы они не сливались на заданной длине и их можно было рассматривать как квазисвободные. Между струй формируется пространство циркуляции масс воздуха, эжектируемых внутренними сторонами струй. Сложный характер направленных движений в циркуляционном пространстве в сочетании с турбулентностью допускает считать там температуру воздуха tц близкой к постоянной. Записывая относительно каждой струи балансовые уравнения вида (11) и преобразовывая их, получим систему
dθ1/(1 - 2θ1) = dε1, dθ2/(1 - 2θ2) = dε2, (15)
где θ1 = (tц – tя1)/(tц – t1),
θ2 = (tя2 – tц)/(t2 – tц), ε1 = α1Fя1/Wя1,
ε2 = α2Fя2/Wя2. Поскольку при х = 0 θ1 = θ2 = 1 решения уравнений (15) имеют вид
Θ1 = 0,5[1 + exp(- 2E1)], Θ2 = 0,5[1 + exp(- 2E2)] (16)
Приравнивая теплопотери
Wя1(tя1 – t1) = Wя2(tя2 – t2)
и выражая температуры tя1 и tя2 через (16), найдем температуру циркуляционного пространства
tц = (t1 + Аt2)/(1 + А) (17)
А = (1 – θ2)Wя2 / (1 – θ1)Wя1
При Wя1 = Wя2, ε1 = ε2, θ1 = θ2 имеем A = 1, а tц = 0,5(t1 + t2).
Пример 2.
Исходные данные, как в примере 1, кроме to1 = t1 = - 30oC, to2 = t2 = 20oC, tц = - 5oC
| х, м | E1 = Е2 | Θ1 = Θ2 | tя1 | tя2 |
| 1 | 0,234 | 0,813 | - 25,3 | 15,3 |
| 2 | 0,343 | 0,752 | - 23,8 | 13,8 |
| 3 | 0,431 | 0,711 | - 22,8 | 12,8 |
| 4 | 0,505 | 0,683 | - 22,1 | 12,1 |
4. Выводы
Привнесение методов конвективного теплообмена и теории теплообменных аппаратов в теорию струй с использованием классических результатов по распределению скоростей и температур в свободных затопленных турбулентных струях позволяет рассчитать теплообмен в разнообразных неклассических случаях. Применимость метода ограничена очевидными рамками, однако при наличии теоретических решений или экспериментальных данных по струйным течениям, отличающимся от свободных затопленных струй, возможно дальнейшее расширение области применения. Можно надеяться в дальнейшем на успешное использование данного метода в расчетах воздушно-тепловых завес.
Использованные источники
1.М.И.Гримитлин. Распределение воздуха в помещениях. Издание 3-е дополненное и исправленное. Издательство «АВОК Северо-Запад».Санкт-Петербург. 2004
2. И.Е.Идельчик. Справочник по гидравлическим сопротивлениям. Госэнергоиздат. М.-Л. 1960




